前回ナゾ010で、日本語ならではの考え方が難しい事が判明。
これが今後どのように作用していくのか?
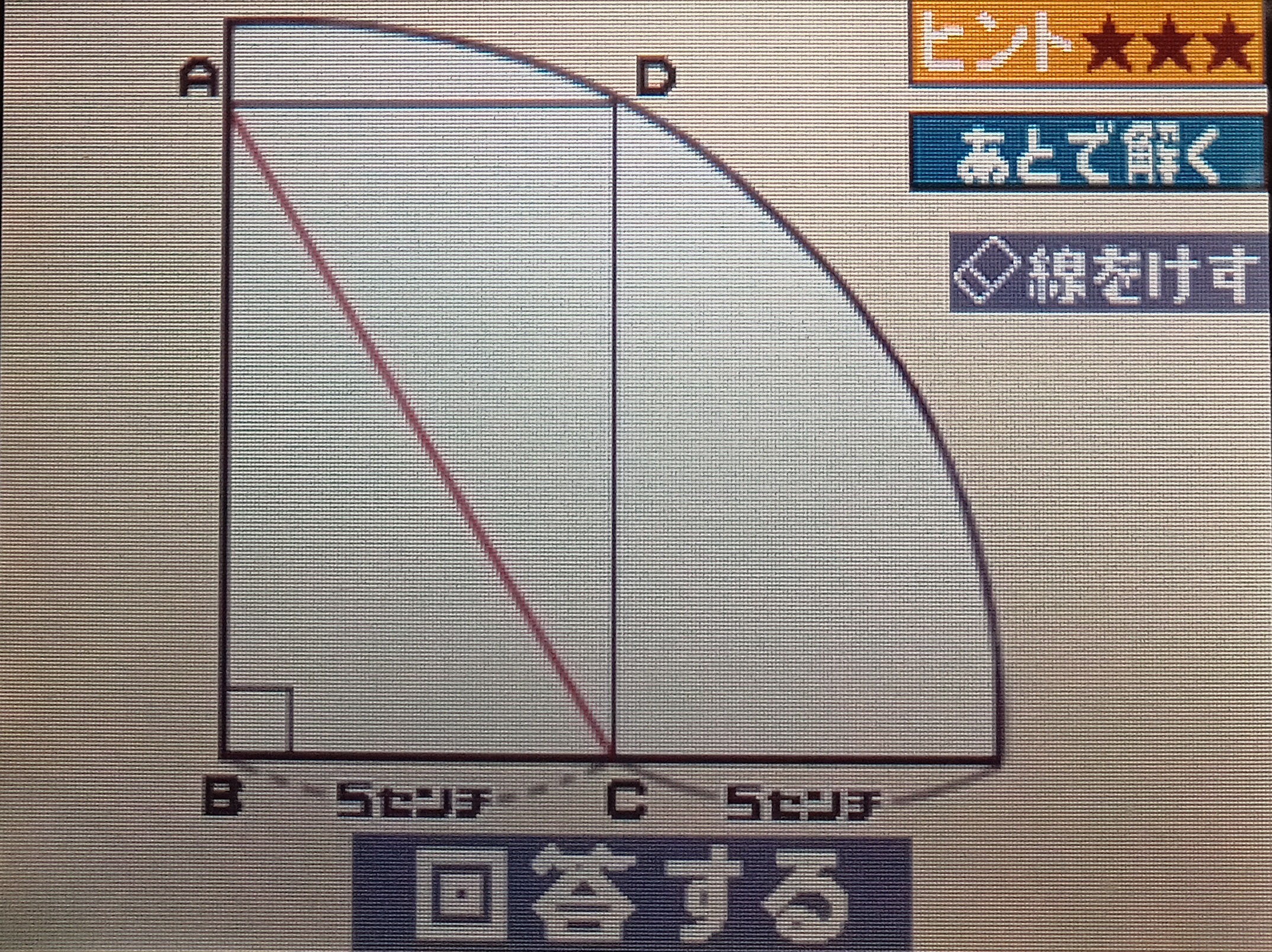
【ナゾ011 円弧と直線】
図のように、4分の1の円に内接している長方形ABCDがある。
Bが円の中心だとして、長方形の対角線ACの長さは何センチだろう。
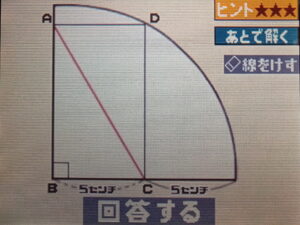
【正解】10センチ
【生成AIによる攻略フェーズ】
初の?図形問題。
だが、ある意味引っかけ問題でもある。
求めたいのはACの長さ。これはBDと同じ長さ。
BDはそのまま円の半径になるので、10センチとなる。
三平方の定理とかこねくり回す必要は無い。が、絶対出てくるはず(笑)
【第1回戦】
▼プロンプト① (※ゲーム原文そのまま)
図のように、4分の1の円に内接している長方形ABCDがある。
Bが円の中心だとして、長方形の対角線ACの長さは何センチだろう。
▼AI回答①
| ChatGPT | Gemini | Copilot | |
|---|---|---|---|
| プロンプト①に 対する生回答の 要約 | ・問題・図形は正しく理解 ・三平方の定理は使わなかったが、変な計算を始めた | ・問題・図形は正しく理解 ・案の定、三平方の定理を使って計算をはじめる ・前提がおかしい箇所がある | ・半径を5cmと誤認識 ・三平方の定理を使って計算をはじめる |
| 最終判断 (原文から) | AC=10cm | 長方形の対角線ACの長さは 5√5 センチです | ということで、対角線ACの長さは5√2 cm! |
| 結果 | ○ 正解! | × 不正解 | × 不正解 |
最近ナリを潜めていたChatGPTくん、貫禄の正解。
計算じゃなくて「AC=BDの長さ」で気付いてくれればもっとカッコよかったけど。
▼まとめと考察
まず、図形問題も対応出来そうなのが解ったのは収穫。
だがGeminiは「点Aと円周上の点Dは、中心Bからの距離が半径に等しいので、
BA=BD=10センチです」
Copilotは「ABとBCがそれぞれ半径だから、どちらも5cm。」
とそれぞれ謎定義を展開。そりゃ答えも間違ってくるよ。
ナゾ001や004でもそうだったけど、もしかするとGeminiとCopilotは画像認識の
ロジックがちと弱いのかもしれない。


コメント